说完了策略梯度算法(PG),我们来谈谈目前更常用的、训练效率和效果更好的近端策略优化(PPO)。
1. PPO推导:
在此之前,我们需要先明白同策略(On-Policy)和异策略(Off-Policy)分别是什么。

如上图所示,原来的PG算法就是On-Policy的典型算法。它的特点是智能体在每次更新策略后,必须使用新策略收集新的经验数据。也就是上图红字所示的,每次迭代得到的多个轨迹数据仅使用一次。毕竟你策略参数都更新了,对应的轨迹概率就不一样了,之前采样出来的数据也就不能用了。
但是On-Policy的算法存在一个问题,就是智能体需要花很多时间去采样数据,可以说大多数时间都在采样数据。
所以为了解决这个问题,我们就需要一种对应的Off-Policy算法。
其实On-Policy和Off-Policy的主要区别就在于如何使用经验(状态、动作、奖励和下一个状态)来更新智能体的策略。
On-Policy: 行动策略和目标策略是同一个策略。
Off-Policy: 行动策略和目标策略不是同一个策略。
而将On-Policy转为Off-Policy的改进思路就是用拥有另外一个策略的另一个演员去跟环境做互动,然后用该演员收集到的数据去训练真正的演员。假设我们可以用另一个演员收集到的数据去训练真正的演员,意味着说我们可以把收集到的数据用很多次,也就是可以执行梯度上升好几次,更新参数好几次,这都只要用同一笔数据就可以实现。
具体的实现和PPO的推导过程见下图:

上图中的TRPO:信任区域策略优化(trust region policy optimization,TRPO)是PPO的前身。TRPO 与 PPO 不一样的地方是约束项摆的位置不一样,PPO 是直接把约束放到要优化的式子里,可以直接用梯度上升的方法最大化这个式子。但TRPO是把 KL 散度当作约束,它希望θ跟θ’的 KL 散度小于一个δ。如果我们使用的是基于梯度的优化时,有约束是很难处理的,因为它把 KL 散度约束当做一个额外的约束,没有放目标里面。PPO 跟 TRPO 的性能差不多,但 PPO 在实现上比 TRPO 容易的多,所以我们一般就用 PPO,而不用TRPO。
接着,我们来介绍一下PPO的一个重要变种:

上式看起来很复杂,其实很简单,它想做的事情就是希望pθ(at |st)跟pθk(at |st),也就是做示范的模型跟实际上学习的模型,在优化以后不要差距太大。
- 操作符min作用是在第一项和第二项中选择最小的。
- 第二项前面有个裁剪(clip)函数,裁剪函数是指:在括号里有三项,如果第一项小于第二项,则输出1 − ε;如果第一项大于第三项的话,则输出1 + ε。
- ε 是一个超参数,要需要我们调整的,一般设置为0.1或0.2 。
clip函数图像:
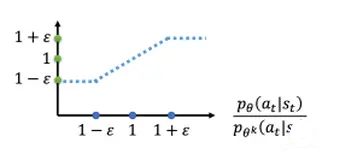
目标函数图像:
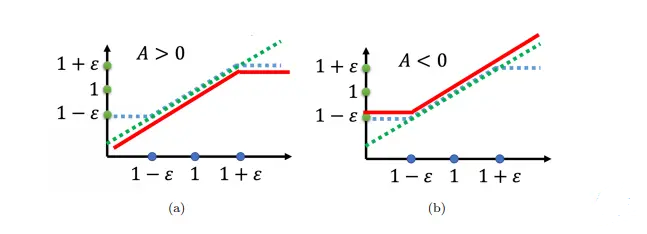
绿线是pθ(at |st)/pθk(at |st),蓝线是clip函数值,在绿线跟蓝线中间,我们要取最小值,所以红线就是目标函数值。
如果 A > 0,也就是某一个状态-动作的对是好的,我们希望增加这个状态-动作对的概率。也就是想要让pθ(at |st)越大越好,但它跟pθk(at |st)的比值不可以超过1+ε。如果超过 1 +ε 的话,就没有好处了。所以在训练的时候,当pθ(at |st)被训练到pθ(at |st)/pθk(at |st)> 1 +ε 时,它就会停止。
同理,如果 A < 0,也就是某一个状态-动作对是不好的,我们就希望把pθ(at |st)减小。如果pθ(at |st)比pθk(at |st)还大,那我们就尽量把它压小,但是压到pθ(at |st)/pθk(at |st)为 1 − ε 的时候就该停了。
2. 代码实现:
class PPO:
def __init__(self, policy_class, env, **hyperparameters):
# PPO 初始化用于训练的超参数
self._init_hyperparameters(hyperparameters)
# 提取环境信息
self.env = env
self.obs_dim = env.observation_space.shape[0]
self.act_dim = env.action_space.shape[0]
# 初始化演员和评论家网络
self.actor = policy_class(self.obs_dim, self.act_dim)
self.critic = policy_class(self.obs_dim, 1)
# 为演员和评论家初始化优化器
self.actor_optim = Adam(self.actor.parameters(), lr=self.lr)
self.critic_optim = Adam(self.critic.parameters(), lr=self.lr)
# 初始化协方差矩阵,用于查询actor网络的action
self.cov_var = torch.full(size=(self.act_dim,), fill_value=0.5)
self.cov_mat = torch.diag(self.cov_var)
def learn(self, total_timesteps):
t_so_far = 0 # 到目前为止仿真的时间步数
i_so_far = 0 # 到目前为止,已运行的迭代次数
while t_so_far < total_timesteps:
# 收集批量实验数据
batch_obs, batch_acts, batch_log_probs, batch_rtgs, batch_lens = self.rollout() # 这里体现的其实是On-Policy
# 计算收集这一批数据的时间步数
t_so_far += np.sum(batch_lens)
# 增加迭代次数
i_so_far += 1
# 计算第k次迭代的advantage
V, _ = self.evaluate(batch_obs, batch_acts)
A_k = batch_rtgs - V.detach()
# 将优势归一化 在理论上不是必须的,但在实践中,它减少了我们优势的方差,使收敛更加稳定和快速。
# 添加这个是因为在没有这个的情况下,解决一些环境的问题太不稳定了。
A_k = (A_k - A_k.mean()) / (A_k.std() + 1e-10)
# 在其中更新我们的网络。(体现Off-Policy)
for _ in range(self.n_updates_per_iteration):
# 从这里开始就是PPO的具体实现
V, curr_log_probs = self.evaluate(batch_obs, batch_acts)
# 重要性采样的权重
ratios = torch.exp(curr_log_probs - batch_log_probs)
surr1 = ratios * A_k
surr2 = torch.clamp(ratios, 1 - self.clip, 1 + self.clip) * A_k
# 计算两个网络的损失。(注意actor_loss实际上是对目标函数值的取反,这样可以将最大化问题变成最小化问题,将目标函数变成损失函数,从而可以兼容pytorch框架里的一些高效方法)
actor_loss = (-torch.min(surr1, surr2)).mean()
critic_loss = nn.MSELoss()(V, batch_rtgs)
# 计算梯度并对actor网络进行反向传播
# 梯度清零
self.actor_optim.zero_grad()
# 反向传播,产生梯度
actor_loss.backward(retain_graph=True)
# 通过梯度下降进行优化
self.actor_optim.step()
# 计算梯度并对critic网络进行反向传播
self.critic_optim.zero_grad()
critic_loss.backward()
self.critic_optim.step()
def rollout(self):
"""
这就是我们从实验中收集一批数据的地方。由于这是一个on-policy的算法,我们需要在每次迭代行为者/批评者网络时收集一批新的数据。
"""
batch_obs = []
batch_acts = []
batch_log_probs = []
batch_rews = []
batch_rtgs = []
batch_lens = []
# 一回合的数据。追踪每一回合的奖励,在回合结束的时候会被清空,开始新的回合。
ep_rews = []
# 追踪到目前为止这批程序我们已经运行了多少个时间段
t = 0
# 继续实验,直到我们每批运行超过或等于指定的时间步数
while t < self.timesteps_per_batch:
ep_rews = [] 每回合收集的奖励
# 重置环境
obs = self.env.reset()
done = False
# 运行一个回合的最大时间为max_timesteps_per_episode的时间步数
for ep_t in range(self.max_timesteps_per_episode):
# 递增时间步数,到目前为止已经运行了这批程序
t += 1
# 追踪本批中的观察结果
batch_obs.append(obs)
# 计算action,并在env中执行一次step。
# 注意,rew是奖励的简称。
action, log_prob = self.get_action(obs)
obs, rew, done, _ = self.env.step(action)
# 追踪最近的奖励、action和action的对数概率
ep_rews.append(rew)
batch_acts.append(action)
batch_log_probs.append(log_prob)
if done:
break
# 追踪本回合的长度和奖励
batch_lens.append(ep_t + 1)
batch_rews.append(ep_rews)
# 将数据重塑为函数描述中指定形状的张量,然后返回
batch_obs = torch.tensor(batch_obs, dtype=torch.float)
batch_acts = torch.tensor(batch_acts, dtype=torch.float)
batch_log_probs = torch.tensor(batch_log_probs, dtype=torch.float)
batch_rtgs = self.compute_rtgs(batch_rews)
return batch_obs, batch_acts, batch_log_probs, batch_rtgs, batch_lens
def compute_rtgs(self, batch_rews):
batch_rtgs = []
# 遍历每一回合,一个回合有一批奖励
for ep_rews in reversed(batch_rews):
# 到目前为止的折扣奖励
discounted_reward = 0
# 遍历这一回合的所有奖励。我们向后退,以便更顺利地计算每一个折现的回报(依然是逆序取)
for rew in reversed(ep_rews):
discounted_reward = rew + discounted_reward * self.gamma
batch_rtgs.insert(0, discounted_reward)
# 将每个回合的折扣奖励的数据转换成张量
batch_rtgs = torch.tensor(batch_rtgs, dtype=torch.float)
return batch_rtgs
def get_action(self, obs):
mean = self.actor(obs)
# 用上述协方差矩阵中的平均行动和标准差创建一个分布。
dist = MultivariateNormal(mean, self.cov_mat)
action = dist.sample()
log_prob = dist.log_prob(action)
return action.detach().numpy(), log_prob.detach()
def evaluate(self, batch_obs, batch_acts):
"""
估算每个观察值,以及最近一批actor网络迭代中的每个action的对数prob。
"""
# 为每个batch_obs查询critic网络的V值。V的形状应与batch_rtgs相同。
V = self.critic(batch_obs).squeeze()
# 使用最近的actor网络计算批量action的对数概率。
mean = self.actor(batch_obs)
dist = MultivariateNormal(mean, self.cov_mat)
log_probs = dist.log_prob(batch_acts)
# 返回批次中每个观察值的值向量V和批次中每个动作的对数概率log_probs
return V, log_probs