8.20：数组-二分查找

题目：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

分析：

这题涉及了使用二分查找的前提条件：1.数组有序 2.数组元素不重复 ，同时使用二分法时必须注意一个关键点：区间的定义（到底是while(left < right) 还是 while(left <= right)），这时我们必须要遵守循环不变量原则，在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，我一般将二分查找的区间定义为[left, right]，即while(left <= right)，这样的话因为[left, right]是闭区间，即每一次查找nums[left]和nums[right]都在查找区间里，所以当开始折半查找时，如果target 在左区间，则折半为[left, middle – 1]，如果target在右区间，则折半为[middle + 1, right]，因为当nums[middle]不等于target时下一个查询区间不会去比较。

答案：

public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target) {
                return mid;
            }
            else if (nums[mid] < target) {
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }
        return -1;

8.21：数组-移除元素、有序数组的平方（双指针法）

题目1-移除元素：

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

分析：

这个题如果直接暴力解的话，可以用类似于冒泡排序一样的双层for循环，时间复杂度在O(n^2)，但是其实可以用一个非常好的算法——双指针法，通过一个快指针和慢指针在一个for循环下完成两个for循环的工作，将时间复杂度降为O(n)。

定义快慢指针

• 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
• 慢指针：指向新数组下标的位置

说白了就是让快指针去找答案数组所需要的元素传给慢指针，慢指针逻辑上指向的其实是那个答案需要的新数组。

答案：

public int removeElement(int[] nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        return slowIndex;
    }

题目2-有序数组的平方：

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

分析：

同样，这题如果要暴力破解的话，可以让每个数平方以后再排序，但是该题使用双指针法后依然可以减少时间复杂度。

数组其实是有序的，只不过负数平方之后可能成为最大数了，那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间，此时可以考虑双指针法了，i指向起始位置，j指向终止位置，定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置，如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; ，如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

答案：

 public int[] sortedSquares(int[] nums) {
        int right = nums.length - 1;
        int left = 0;
        int[] result = new int[nums.length];
        int index = result.length - 1;
        while (left <= right) {
            if (nums[left] * nums[left] > nums[right] * nums[right]) {
                result[index--] = nums[left] * nums[left];
                ++left;
            } else {
                result[index--] = nums[right] * nums[right];
                --right;
            }
        }
        return result;
    }

8.22：数组-长度最小的子数组、最小覆盖子串（滑动窗口）

题目1-长度最小的子数组：

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

分析：

这道题目暴力解法依然是两个for循环，但时间复杂度为O(n^2)，在leetcode上超时了，于是引出了数组操作中另一个重要的方法：滑动窗口。

滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。其实所谓滑动窗口也是一种双指针法，一个指针指向滑动窗口的起始位置，另一个指向终止位置，不满足条件时，末指针前移扩大窗口，满足条件时，头指针前移缩小窗口，其精髓就是根据当前子序列的情况不断调节子序列的起始位置，从而将O(n^2)降为O(n)。

答案：

public int minSubArrayLen(int s, int[] nums) {
        int left = 0;
        int sum = 0;
        int result = Integer.MAX_VALUE;
        for (int right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= s) {
                result = Math.min(result, right - left + 1);
                sum -= nums[left++];
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;

题目2：

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

分析：

较难，但本质上还是滑动窗口，建议用多种实现做一做。

答案：

8.23：数组-区间和、开发商购买土地（前缀和）

题目1-区间和：

给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

输入描述

第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间，直至文件结束。

输出描述

输出每个指定区间内元素的总和。

题目2-开发商购买土地：

在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。

为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。

分析：

首先，必须要审清，这两题都是在求区间和，而 前缀和 在涉及计算区间和的问题时非常有用。

所谓前缀和，其实就是先把前n个区间的累加和算好，之后每次求区间时只需要将两个区间相减就行，其思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。

举个例子：

p[1] = vec[0] + vec[1];

p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];

p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

于是我们得到了下标2到下标5之间的累加和。

特别注意： 在使用前缀和求解的时候，要特别注意 求解区间。

像刚刚那个例子，如果我们要求 区间下标 [2, 5] 的区间和，那么应该是 p[5] – p[1]，而不是 p[5] – p[2]。

答案1：

public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int[] vec = new int[n];
        int[] p = new int[n];

        int presum = 0;
        for (int i = 0; i < n; i++) {
            vec[i] = scanner.nextInt();
            presum += vec[i];
            p[i] = presum;
        }

        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();

            int sum;
            if (a == 0) {
                sum = p[b];
            } else {
                sum = p[b] - p[a - 1];
            }
            System.out.println(sum);
        }

        scanner.close();
    }

答案2：

public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int sum = 0;
        int[][] vec = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                vec[i][j] = scanner.nextInt();
                sum += vec[i][j];
            }
        }

        // 统计横向
        int[] horizontal = new int[n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                horizontal[i] += vec[i][j];
            }
        }

        // 统计纵向
        int[] vertical = new int[m];
        for (int j = 0; j < m; j++) {
            for (int i = 0; i < n; i++) {
                vertical[j] += vec[i][j];
            }
        }

        int result = Integer.MAX_VALUE;
        int horizontalCut = 0;
        for (int i = 0; i < n; i++) {
            horizontalCut += horizontal[i];
            result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
        }

        int verticalCut = 0;
        for (int j = 0; j < m; j++) {
            verticalCut += vertical[j];
            result = Math.min(result, Math.abs(sum - 2 * verticalCut));
        }

        System.out.println(result);
        scanner.close();
    }

8.24 ~ 8.31：链表的基本操作实现

分析：

链表的一些基本操作还是挺基础的，涉及的算法不算多，有些数据结构课上也都有实现，有必要时复习一下就好。注意，虚拟头结点需要重点了解一下，包括双指针的一些应用。

相关资料：

代码随想录-链表 or 大话数据结构

9.1：环形链表（了解一下）

题目：

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

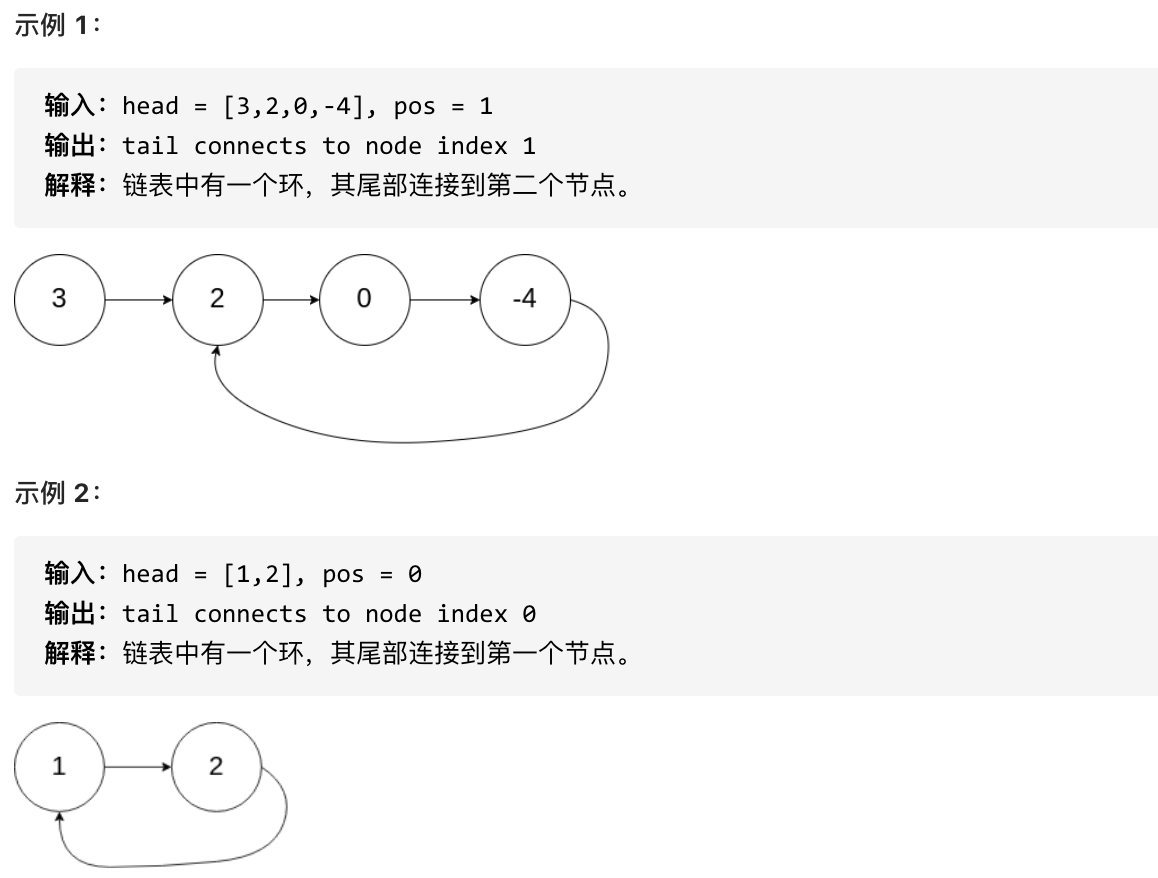
分析：

详细可见 代码随想录-环形链表II

答案：

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {// 有环
                ListNode index1 = fast;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

9.2：哈希表-有效的字母异位词

题目：

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true

示例 2: 输入: s = “rat”, t = “car” 输出: false

说明: 你可以假设字符串只包含小写字母。

分析：

先看暴力的解法，两层for循环，同时还要记录字符是否重复出现，很明显时间复杂度是 O(n^2)。

接下来看优化的方法：数组其实就是一个简单哈希表，而且这道题目中字符串只有小写字符，那么就可以定义一个数组，来记录字符串s里字符出现的次数。定义一个数组叫做record用来记录字符串s里字符出现的次数，即把字符映射到数组也就是哈希表的索引下标上。在遍历字符串t的时候，对t中出现的字符映射哈希表索引上的数值再做-1的操作。最后检查一下，record数组如果有的元素不为零，说明字符串s和t一定是谁多了字符或者谁少了字符，return false。最后如果record数组所有元素都为零，说明字符串s和t是字母异位词，return true。

答案：

public boolean isAnagram(String s, String t) {
        int[] record = new int[26];

        for (int i = 0; i < s.length(); i++) {
            record[s.charAt(i) - 'a']++;
        }

        for (int i = 0; i < t.length(); i++) {
            record[t.charAt(i) - 'a']--;
        }

        for (int count: record) {
            if (count != 0) {
                return false;
            }
        }
        return true;
}

9.3：哈希表-两个数组的交集

题目：

给定两个数组，编写一个函数来计算它们的交集。

说明： 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。

分析：

这道题目，主要目的是学会判断什么时候用数组做哈希表，什么时候用HashMap或HashSet做哈希表。

注意题目特意说明：输出结果中的每个元素一定是唯一的，也就是说输出的结果的去重的， 同时不考虑输出结果的顺序，也就是说输出的结果还是无序的。去重+无序，显然要使用哈希表解答。

虽然用数组来做哈希表是不错的选择，而且如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。之前使用数组来做哈希的题目，是因为题目都限制了数值的大小，而这道题目没有限制数值的大小，就无法使用数组来做哈希表了。

答案：

public int[] intersection(int[] nums1, int[] nums2) {
        if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) {
            return new int[0];
        }
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> resSet = new HashSet<>();
        // 遍历数组1
        for (int i : nums1) {
            set1.add(i);
        }
        // 遍历数组2的过程中判断哈希表中是否存在该元素
        for (int i : nums2) {
            if (set1.contains(i)) {
                resSet.add(i);
            }
        }
        // x -> x 代表直接返回 Integer 类型的原始值
        return resSet.stream().mapToInt(x -> x).toArray();
}

9.4：哈希表-快乐数

题目：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。如果 可以变为  1，那么这个数就是快乐数。

如果 n 是快乐数就返回 True ；不是，则返回 False 。

示例：

输入：19
输出：true
解释：
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1

分析：

这道题的关键在于：无限循环。这意味着：求和的过程中，sum会重复出现。

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法了。

答案：

class Solution {
    public boolean isHappy(int n) {
        Set<Integer> record = new HashSet<>();
        while (n != 1 && !record.contains(n)) {
            record.add(n);
            n = getNextNumber(n);
        }
        return n == 1;
    }

    private int getNextNumber(int n) {
        int res = 0;
        while (n > 0) {
            int temp = n % 10;
            res += temp * temp;
            n = n / 10;
        }
        return res;
    }
}

9.5：哈希表-两数之和（梦开始的地方）

题目：

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9

所以返回 [0, 1]

分析：

很明显暴力的解法是两层for循环查找，时间复杂度是O(n^2)。

什么时候使用哈希法：当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

本题就需要一个集合来存放我们遍历过的元素，然后在遍历数组的时候去询问这个集合，某元素是否遍历过，也就是是否出现在这个集合。而且，本题我们不仅要知道元素有没有遍历过，还要知道这个元素对应的下标，需要使用 key value结构来存放，key来存元素，value来存下标，那么使用map正合适。

以下是本题的思路图：

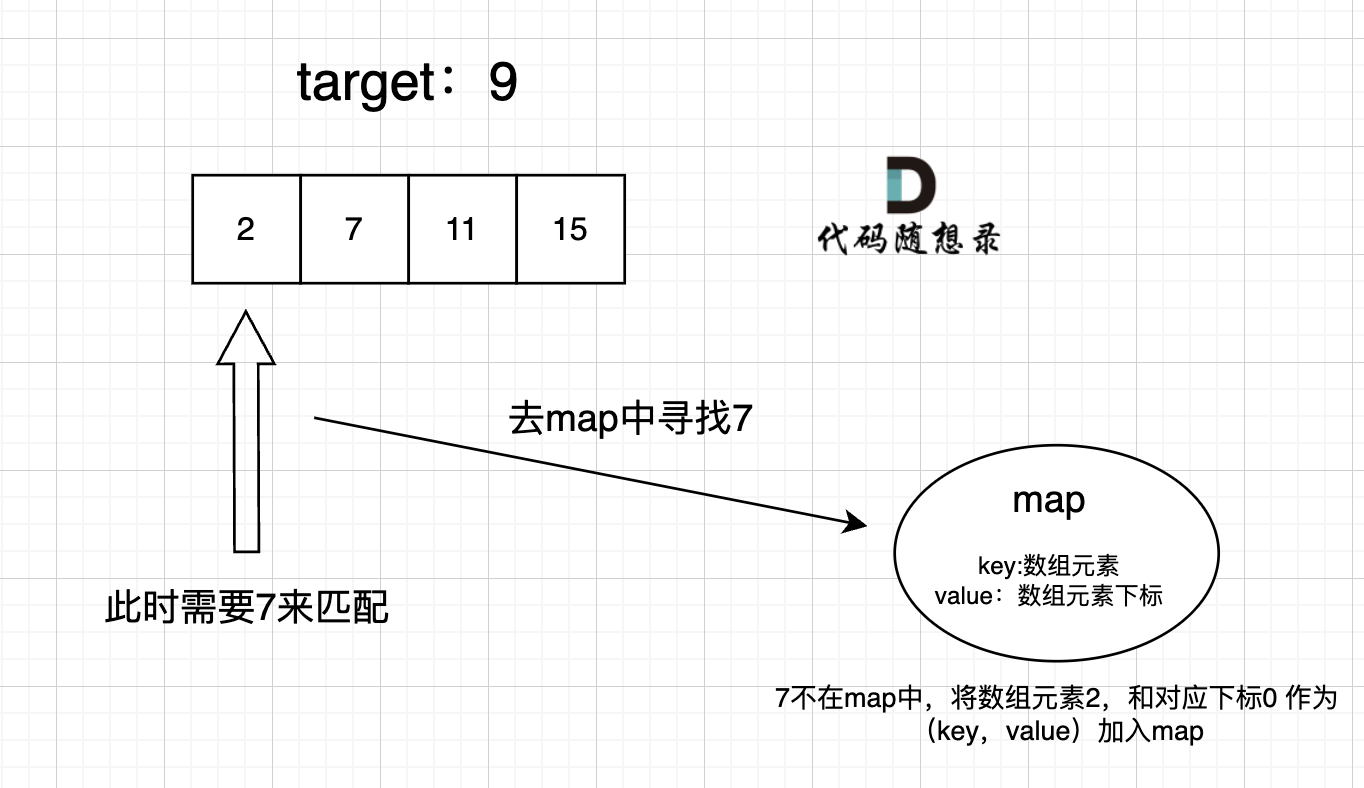
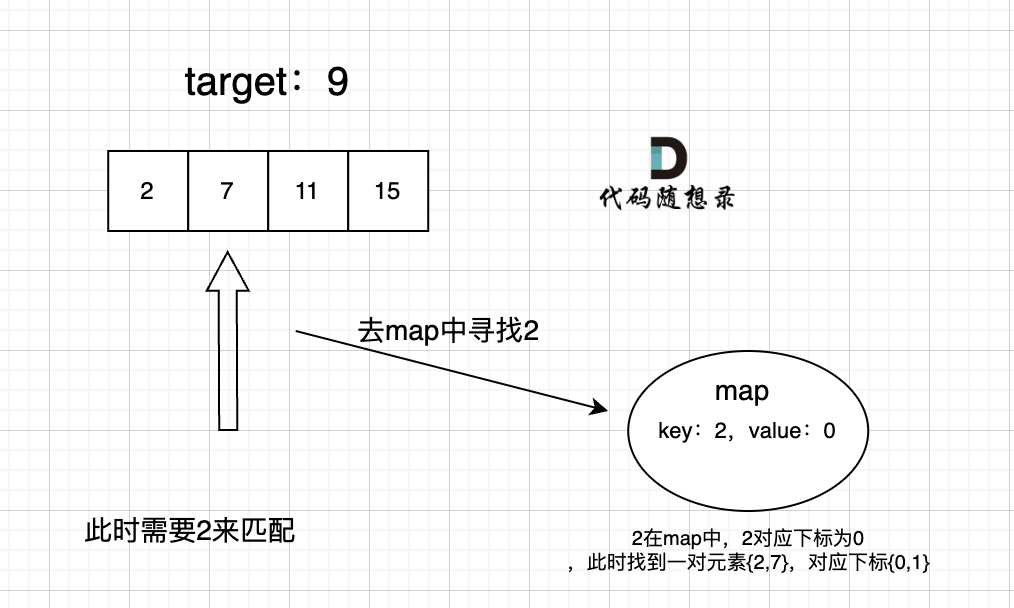
答案：

public int[] twoSum(int[] nums, int target) {
    int[] res = new int[2];
    if(nums == null || nums.length == 0){
        return res;
    }
    Map<Integer, Integer> map = new HashMap<>();
    for(int i = 0; i < nums.length; i++){
        int temp = target - nums[i];   // 遍历当前元素，并在map中寻找是否有匹配的key
        if(map.containsKey(temp)){
            res[1] = i;
            res[0] = map.get(temp);
            break;
        }
        map.put(nums[i], i);    // 如果没找到匹配对，就把访问过的元素和下标加入到map中
    }
    return res;
}

9.6：哈希表-四数相加II

题目：

给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。

为了使问题简单化，所有的 A, B, C, D 具有相同的长度 N，且 0 ≤ N ≤ 500 。所有整数的范围在 -2^28 到 2^28 – 1 之间，最终结果不会超过 2^31 – 1 。

示例：

输入:

• A = [ 1, 2]
• B = [-2,-1]
• C = [-1, 2]
• D = [ 0, 2]

输出:

2

解释:

两个元组如下:

1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

分析：

这道题其实延用了上题 两数之和 的思路，就是题目拗口了一点，本质上就是求两数之和，看下面的解题步骤就能明白。

1. 首先定义 一个map，key放a和b两数之和，value 放a和b两数之和出现的次数。
2. 遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中。
3. 定义int变量count，用来统计 a+b+c+d = 0 出现的次数。
4. 再遍历大C和大D数组，找到如果 0-(c+d) 在map中出现过的话，就用count把map中key对应的value也就是出现次数统计出来。
5. 最后返回统计值 count 就可以了

答案：

class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        int res = 0;
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        //统计两个数组中的元素之和，同时统计出现的次数，放入map
        for (int i : nums1) {
            for (int j : nums2) {
                int sum = i + j;
                map.put(sum, map.getOrDefault(sum, 0) + 1);
            }
        }
        //统计剩余的两个元素的和，在map中找是否存在相加为0的情况，同时记录次数
        for (int i : nums3) {
            for (int j : nums4) {
                res += map.getOrDefault(0 - i - j, 0);
            }
        }
        return res;
    }
}

9.7：哈希表-赎金信

题目：

给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成，返回 true ；否则返回 false。

• 杂志字符串中的每个字符只能在赎金信字符串中使用一次。
• 你可以假设两个字符串均只含有小写字母。

示例：

canConstruct(“a”, “b”) -> false
canConstruct(“aa”, “ab”) -> false
canConstruct(“aa”, “aab”) -> true

分析：

这题可以用两层for循环暴力破解：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        for (int i = 0; i < magazine.length(); i++) {
            for (int j = 0; j < ransomNote.length(); j++) {
                // 在ransomNote中找到和magazine相同的字符
                if (magazine[i] == ransomNote[j]) {
                    ransomNote.erase(ransomNote.begin() + j); // ransomNote删除这个字符
                    break;
                }
            }
        }
        // 如果ransomNote为空，则说明magazine的字符可以组成ransomNote
        if (ransomNote.length() == 0) {
            return true;
        }
        return false;
    }
};

但是，复杂度为O(n^2)，还是比较高的。

所以，我们可以采用空间换取时间的哈希策略，用一个长度为26的数组来记录magazine里字母出现的次数，然后再用ransomNote去验证这个数组是否包含了ransomNote所需要的所有字母。这依然是数组在哈希法中的应用。

注意：使用map的空间消耗要比数组大一些，因为map要维护红黑树或者哈希表，而且还要做哈希函数，是费时的，数据量大的话就能体现出来差别了。 所以数组更加简单直接有效。简而言之，能用数组用数组。

答案：

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        int record[26] = {0};
        //add
        if (ransomNote.size() > magazine.size()) {
            return false;
        }
        for (int i = 0; i < magazine.length(); i++) {
            // 通过record数据记录 magazine里各个字符出现次数
            record[magazine[i]-'a'] ++;
        }
        for (int j = 0; j < ransomNote.length(); j++) {
            // 遍历ransomNote，在record里对应的字符个数做--操作
            record[ransomNote[j]-'a']--;
            // 如果小于零说明ransomNote里出现的字符，magazine没有
            if(record[ransomNote[j]-'a'] < 0) {
                return false;
            }
        }
        return true;
    }
};

10.27：二叉树-路径总和I、路径总和II

分析：

这两题放在一起做其实告诉了我们一个可能的规律：

在递归三部曲中的第一步-确定递归函数的参数和返回类型时，什么时候需要返回值？什么时候不需要返回值？

这里总结以下三种情况：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（路径总和II）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
• 如果只需要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（路径总和I）

接着，递归第二步-确认终止条件：用递减，让计数器count初始为目标和，如果最后count == 0，同时到了叶子节点的话，说明找到了目标和，如果遍历到了叶子节点，count不为0，就是没找到。

最后，递归第三步-确定单层递归的逻辑。

题目1-路径总和I：

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

答案：

public boolean haspathsum(treenode root, int targetsum) {
        if (root == null) {
            return false;
        }
        targetsum -= root.val;
        if (root.left == null && root.right == null) {
            return targetsum == 0;
        }
        if (root.left != null) {
            if (haspathsum(root.left, targetsum)) {
                return true;
            }
        }
        if (root.right != null) {
            if (haspathsum(root.right, targetsum)) {
                return true;
            }
        }
        return false;
    }

10.28：二叉树-从中序与后序遍历序列构造二叉树、最大二叉树（构造二叉树）

题目1-从中序与后序遍历序列构造二叉树：

根据一棵树的中序遍历与后序遍历构造二叉树。注意: 你可以假设树中没有重复的元素。

分析：

以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。如图所示：

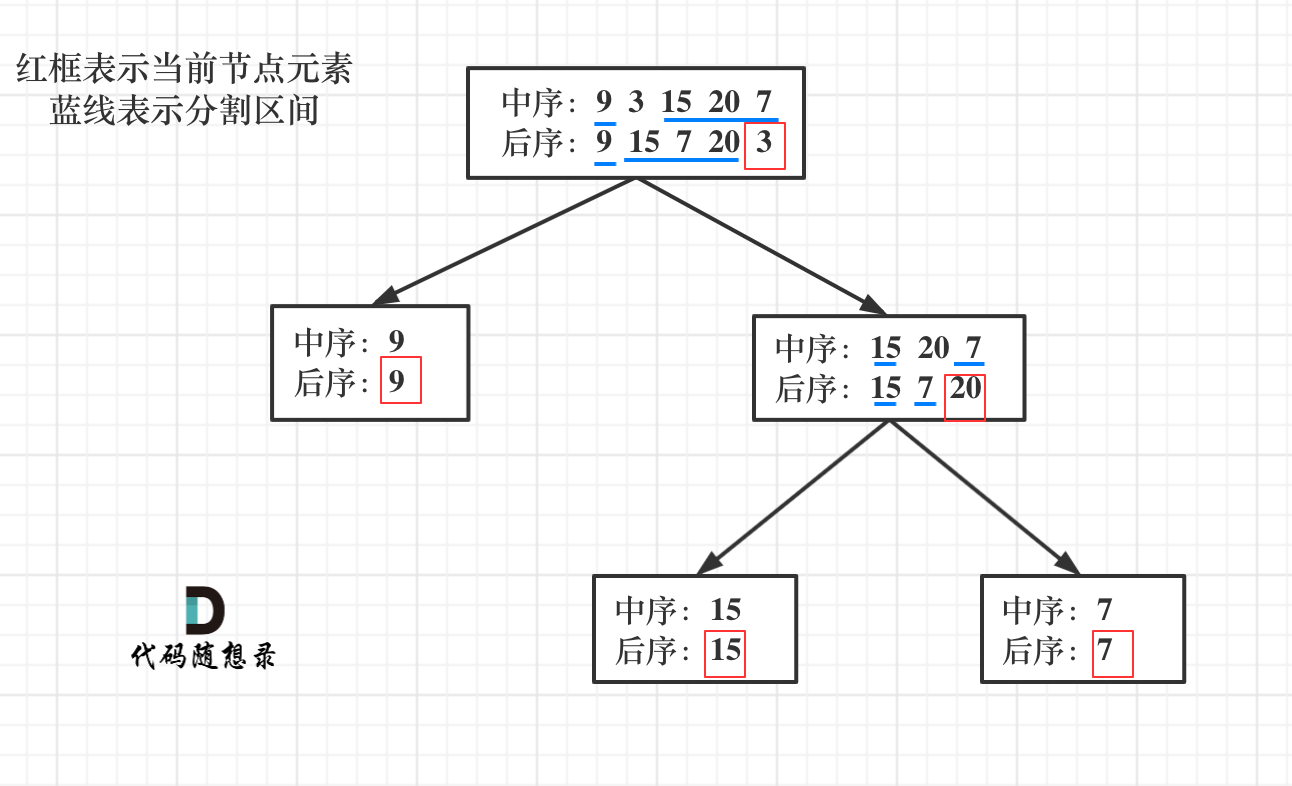
答案：

注意：通过 中序和后序遍历、中序和前序遍历 都是可以构造出正确的二叉树的，但是前序和后序遍历不行。

题目2-最大二叉树：

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

• 二叉树的根是数组中的最大元素。
• 左子树是通过数组中最大值左边部分构造出的最大二叉树。
• 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

分析：

递归三部曲，根据一些特殊的终止情况写终止条件，和上一题比起来简单多了。

答案：

10.29：二叉树-对称二叉树、合并二叉树（同时操作两颗二叉树）

题目1-对称二叉树：

给定一个二叉树，检查它是否是镜像对称的。

分析：

递归三部曲，同时遍历根节点的左子树和右子树，实际上就是同时遍历两个二叉树，检查他们的内外节点是否一致，难度不大。

答案：

1.递归法

public boolean isSymmetric(TreeNode root) {
        return compare(root.left, root.right);
    }

    private boolean compare(TreeNode left, TreeNode right) {

        if (left == null && right != null) {
            return false;
        }
        if (left != null && right == null) {
            return false;
        }

        if (left == null && right == null) {
            return true;
        }
        if (left.val != right.val) {
            return false;
        }
        // 比较外侧
        boolean compareOutside = compare(left.left, right.right);
        // 比较内侧
        boolean compareInside = compare(left.right, right.left);
        return compareOutside && compareInside;
    }

2.迭代法-使用双端队列Deque<TreeNode>，相当于两个栈（这个数据结构很重要）

public boolean isSymmetric2(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.pollFirst();
            TreeNode rightNode = deque.pollLast();
            if (leftNode == null && rightNode == null) {
                continue;
            }
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            deque.offerFirst(leftNode.left);
            deque.offerFirst(leftNode.right);
            deque.offerLast(rightNode.right);
            deque.offerLast(rightNode.left);
        }
        return true;
    }

题目2-合并二叉树：

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

分析：

同时操作两颗二叉树的典例，比较简单。

答案：

1.递归法

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 == null) return root1;

        root1.val += root2.val;
        root1.left = mergeTrees(root1.left,root2.left);
        root1.right = mergeTrees(root1.right,root2.right);
        return root1;
    }

2.迭代法

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 ==null) return root1;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root1);
        queue.offer(root2);
        while (!queue.isEmpty()) {
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();
            // 此时两个节点一定不为空，val相加
            node1.val = node1.val + node2.val;
            // 如果两棵树左节点都不为空，加入队列
            if (node1.left != null && node2.left != null) {
                queue.offer(node1.left);
                queue.offer(node2.left);
            }
            // 如果两棵树右节点都不为空，加入队列
            if (node1.right != null && node2.right != null) {
                queue.offer(node1.right);
                queue.offer(node2.right);
            }
            // 若node1的左节点为空，直接赋值
            if (node1.left == null && node2.left != null) {
                node1.left = node2.left;
            }
            // 若node1的右节点为空，直接赋值
            if (node1.right == null && node2.right != null) {
                node1.right = node2.right;
            }
        }
        return root1;