12.7:贪心算法-分发饼干
题目:
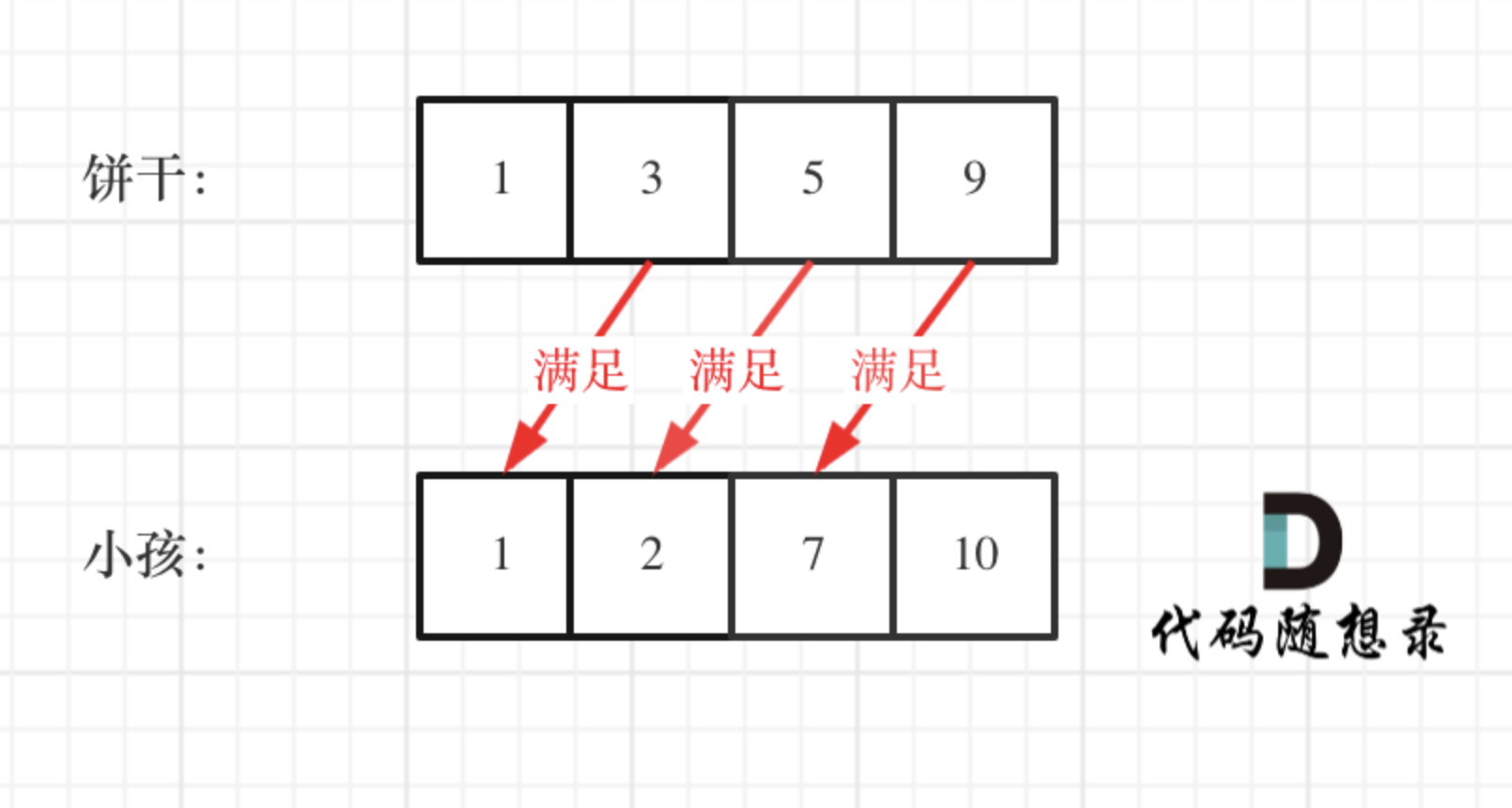
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
- 输入: g = [1,2,3], s = [1,1]
- 输出: 1 解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
示例 2:
- 输入: g = [1,2], s = [1,2,3]
- 输出: 2
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
分析:
贪心算法没有固定的模版和套路,其实我觉得想到贪心主要靠感觉()。想清楚局部最优,想清楚全局最优,感觉局部最优是可以推出全局最优,并想不出反例,那么就试一试贪心。
这题的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
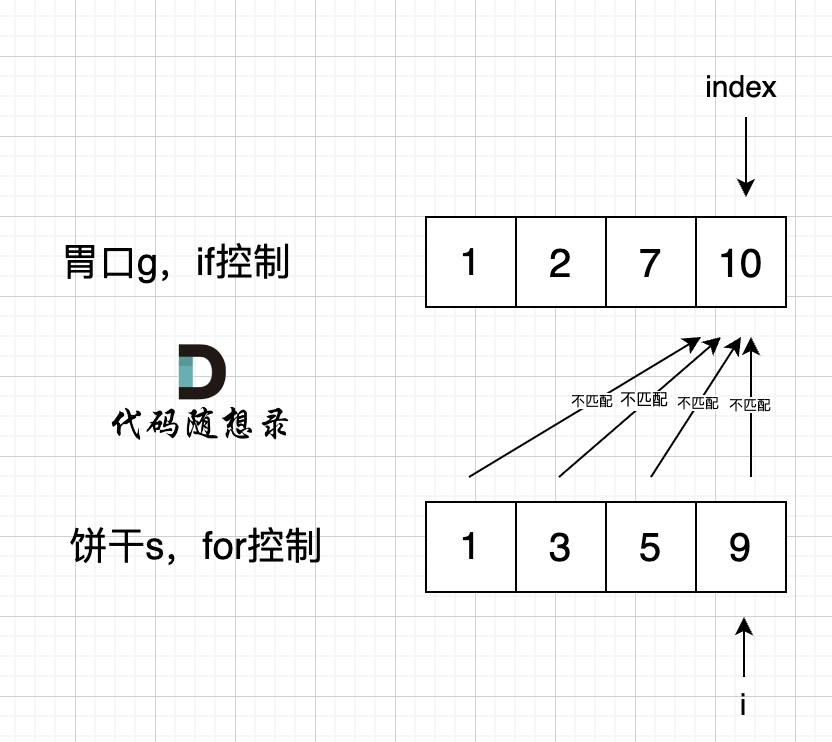
先将饼干数组和小孩数组排序,然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量即可。
注意,要先遍历胃口,再遍历饼干。如果反过来先遍历饼干,再遍历胃口,就会出现以下情况:
答案:
class Solution { public int findContentChildren(int[] g, int[] s) { Arrays.sort(g); Arrays.sort(s); int count = 0; int index = s.length - 1; // 注意几个等号(反向遍历和两个条件判断) for(int i = g.length - 1; i >= 0; i--){ if(index >= 0 && s[index] >= g[i]){ count++; index--; } } return count; }}12.9:贪心算法-摆动序列(较难)
题目:
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
- 输入: [1,7,4,9,2,5]
- 输出: 6
- 解释: 整个序列均为摆动序列。
示例 2:
- 输入: [1,17,5,10,13,15,10,5,16,8]
- 输出: 7
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
分析:
既然题目要求删除元素使其达到最大摆动序列,那么我们必须考虑怎么个删法。拿示例 2 举例,如图所示:
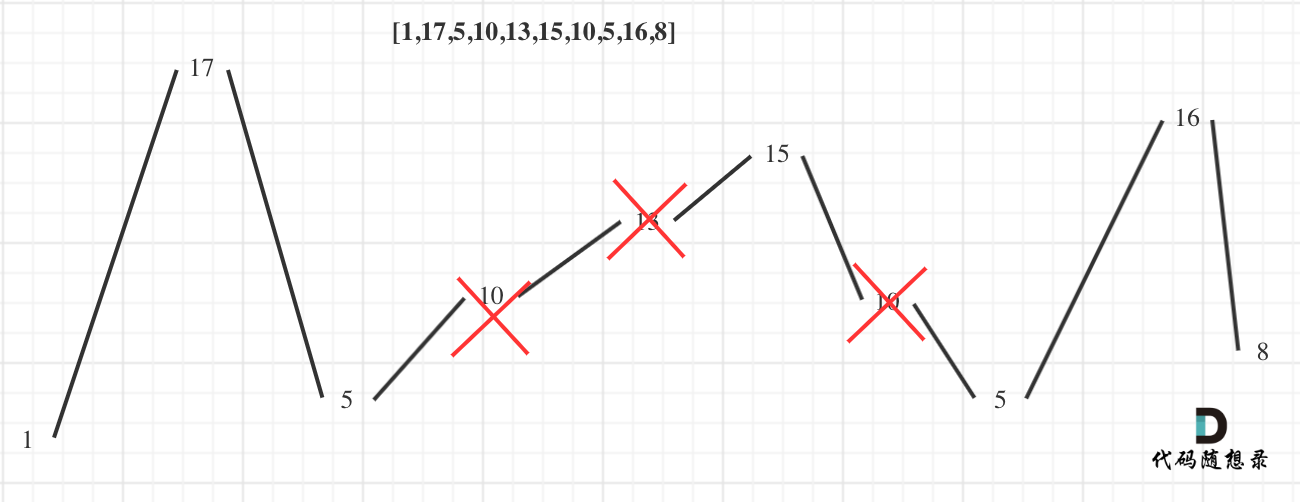
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部极值点。
整体最优:整个序列有最多的局部极值点,从而达到最长摆动序列。
局部最优推出全局最优,并举不出反例,那么试试贪心!
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的极值点数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)。这就是贪心所贪的地方,让极值点尽可能的保持极值点,然后删除单一坡度上的节点。
判断是否有极值点,只需要计算 prediff(nums[i] – nums[i-1]) 和 curdiff(nums[i+1] – nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有极值点需要统计。
这就是我们解决本题的一个大体思路,但是本题有很多要考虑的细节,主要分为以下三种情况:
- 上下坡中有平坡
- 数组首尾两端
- 单调坡中有平坡
情况一:上下坡中有平坡
例如 [1,2,2,2,1]这样的数组:
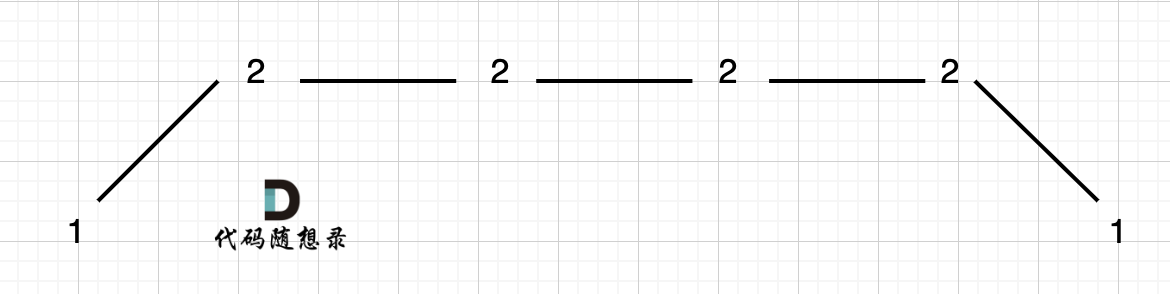
它的摇摆序列长度是3,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。这里我们统一规则,删除左边三个 2 :
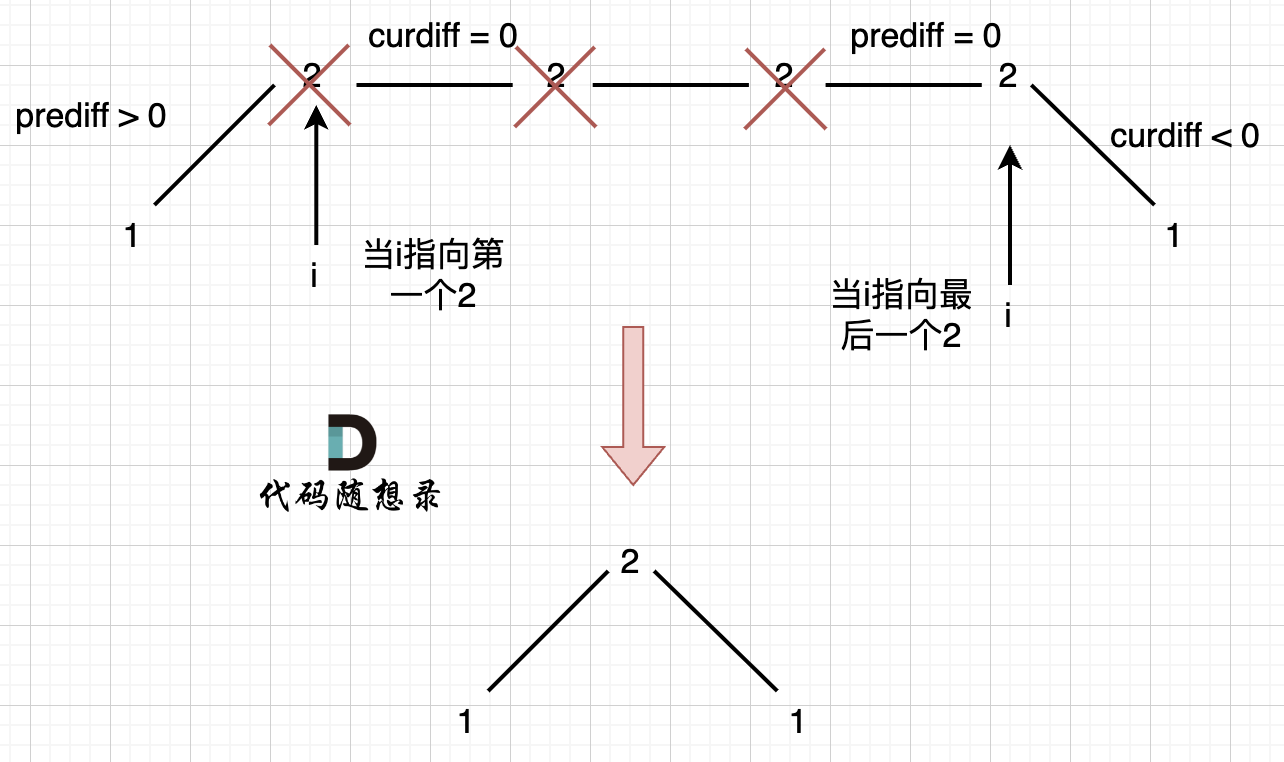
在图中,当 i 指向第一个 2 的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
如果我们采用删左边三个 2 的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个极值点,因为他是把之前相同的元素都删掉留下的极值点。
所以我们记录极值点的条件应修改为: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)
情况二:数组首尾两端
这里主要考虑的是题目中说的,如果只有两个不同的元素,那摆动序列也是 2。例如序列[2,5]。而我们在计算 prediff(nums[i] – nums[i-1]) 和 curdiff(nums[i+1] – nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。这里我们可以写死,就是如果只有两个元素,且元素不同,那么结果为 2。不写死的话,如何将该特殊情况和我们的判断规则结合在一起呢?可以假设,数组最前面还有一个与第一个数字相同的数字。而之前我们在讨论情况一时规定:相同数字连续的时候, prediff = 0 && curdiff < 0 或者 >0 也记为极值点。所以在该假设下,左边极值点会被记录。接着,我们将 result 初始为 1,就是默认记录最右边的极值点。
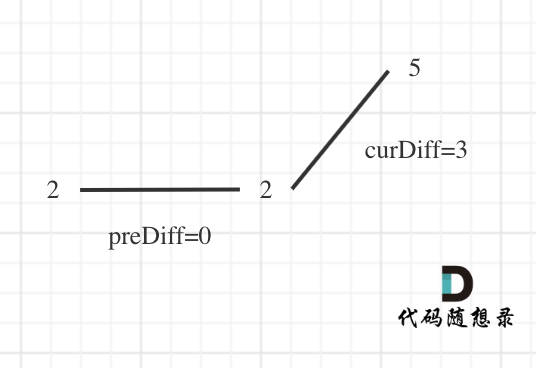
如上图所示,此时 curDiff > 0 && preDiff <= 0,那么 result++,最后得到的 result 就是 2(包含了首尾两个极值点)。
情况三:单调坡度有平坡
在情况一中,我们忽略了一种情况,如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
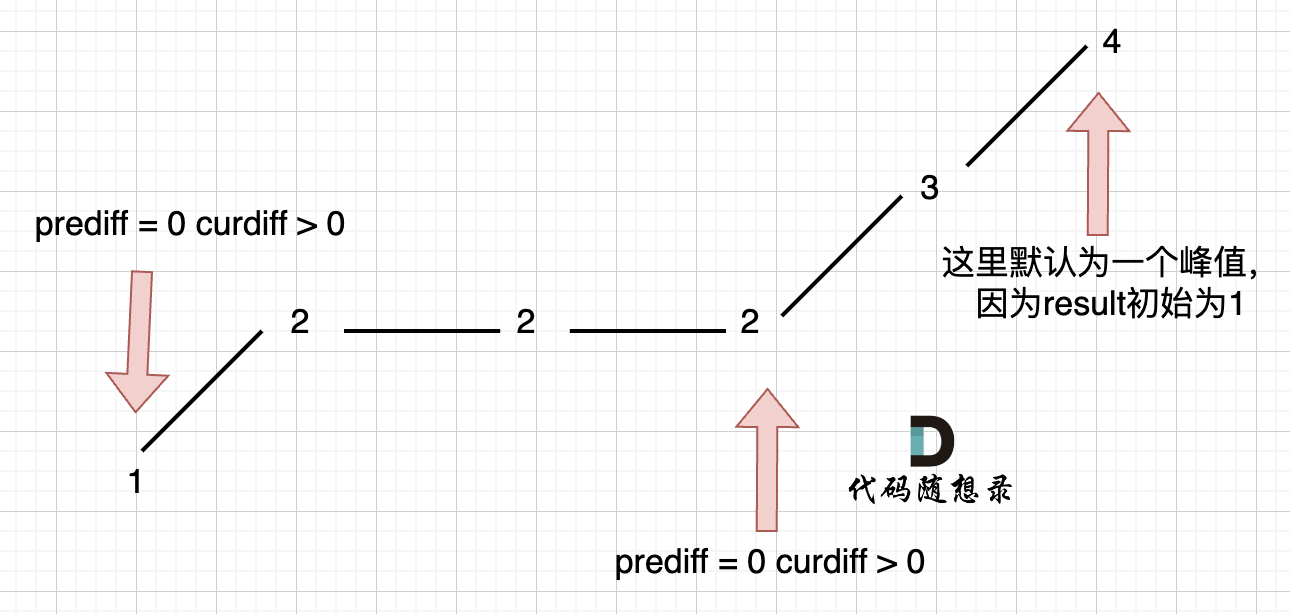
图中,我们可以看出,按照情况一的规则会在三个地方记录极值点,但结果其实是 2,因为单调中的平坡不能算作极值点(即平坡最右边的 2)。
而之所以会出现这个问题,是因为我们实时更新了 prediff。
那么我们应该什么时候更新 prediff 呢?
我们只需要在这个坡度摆动确实发生变化的时候,更新 prediff 就行,这样 prediff 在单调区间有平坡的时候就不会发生变化,造成我们的误判。即将原本随循环实时更新的 prediff,放入判断极值点的 if 语句里即可,非常之巧妙。具体可见代码。
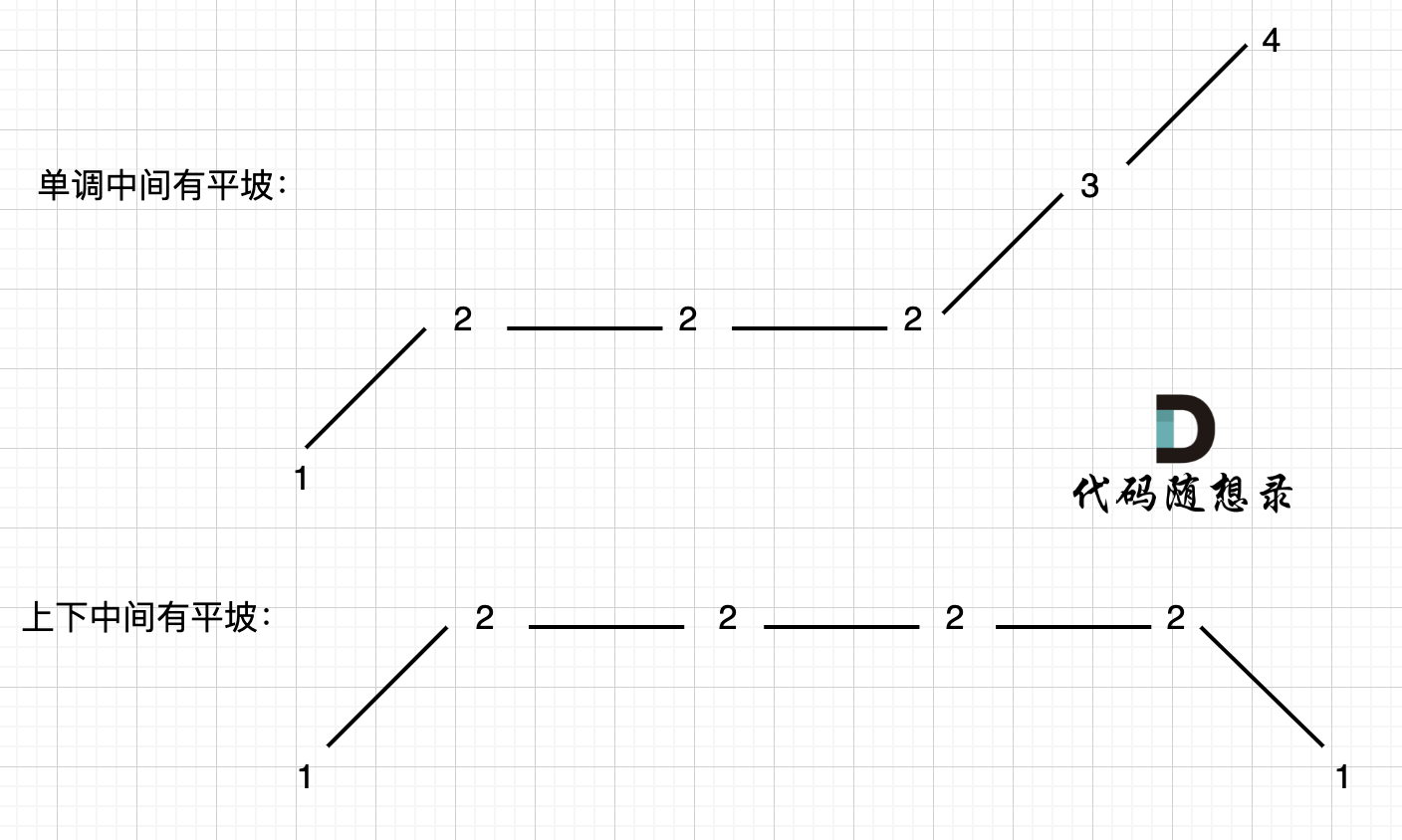
综上所述,本题异常情况的本质,就是要考虑平坡(主要)。平坡分两种,一个是上下中间有平坡,一个是单调中间有平坡,如图:
答案:
class Solution { public int wiggleMaxLength(int[] nums) { if(nums.length < 2){ return nums.length; } int preDiff = 0, curDiff = 0; int count = 1; for(int i = 0; i < nums.length - 1; i++){ curDiff = nums[i + 1] - nums[i]; if(preDiff <= 0 && curDiff > 0 || preDiff >= 0 && curDiff < 0){ count++; preDiff = curDiff; } } return count; }}12.10:贪心算法-最大子序和(有点难想)
题目:
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为6。
分析:
这题用暴力解法勉强可以过,暴力解法的思路:第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值。
那么如果使用贪心,贪哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。相反,只要连续和还是正数就会对后面的元素起到增大总和的作用。,所以只要连续和为正数我们就保留。
全局最优:选取最大“连续和”。

注意,“放弃”负数连续和的方式是将连续和置零。这一点比较巧妙。
答案:
class Solution { public int maxSubArray(int[] nums) { if(nums.length == 1){ return nums[0]; } int res = Integer.MIN_VALUE; int sum = 0; for(int i = 0; i < nums.length; i++){ sum += nums[i]; // 时刻记录最大值 if(sum > res){ res = sum; } // 相当于重置最大子序的起始位置 if(sum < 0){ sum = 0; } } return res; }}12.11:贪心算法-买卖股票的最佳时机II
题目:
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
- 输入: [7,1,5,3,6,4]
- 输出: 7
- 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
- 输入: [1,2,3,4,5]
- 输出: 4
- 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
- 输入: [7,6,4,3,1]
- 输出: 0
- 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
分析:
首先,这道题要想清楚:获得利润至少要两天为一个交易单元。
然后,这道题最关键的是:想到并理解利润拆分。这种拆分方法和前缀和的思路非常像:
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] – prices[0]。
相当于(prices[3] – prices[2]) + (prices[2] – prices[1]) + (prices[1] – prices[0])。
此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑。
那么根据 prices 可以得到每天的利润序列:(prices[i] – prices[i – 1])…..(prices[1] – prices[0])。
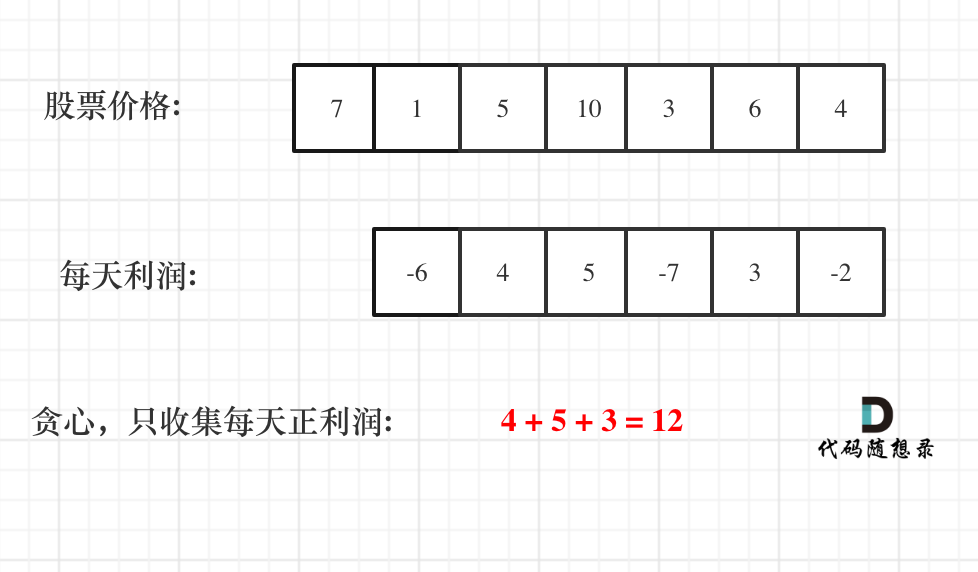
注意,第一天没有利润,至少要第二天才会有利润,所以利润的序列比股票序列少一天。
从图中可以发现,我们只需收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
所以只收集正利润就是贪心所贪的地方。
局部最优:收集每天的正利润。
全局最优:求得最大利润。
局部最优可以推出全局最优,找不出反例,试一试贪心!
答案:
class Solution { public int maxProfit(int[] prices) { int res = 0; for(int i = 1; i < prices.length; i++){ res += Math.max(prices[i] - prices[i - 1], 0); } return res; }}12.16:贪心算法-跳跃游戏
题目:
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1:
- 输入: [2,3,1,1,4]
- 输出: true
- 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
示例 2:
- 输入: [3,2,1,0,4]
- 输出: false
- 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
分析:
刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
其实跳几步无所谓,关键在于可跳的覆盖范围!
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。这个范围内,别管是怎么跳的,反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点。
局部最优:每次取最大跳跃步数,获得最大跳跃范围。
整体最优:得到整体最大覆盖范围,看是否能到终点。
局部最优推出全局最优,找不出反例,试试贪心!
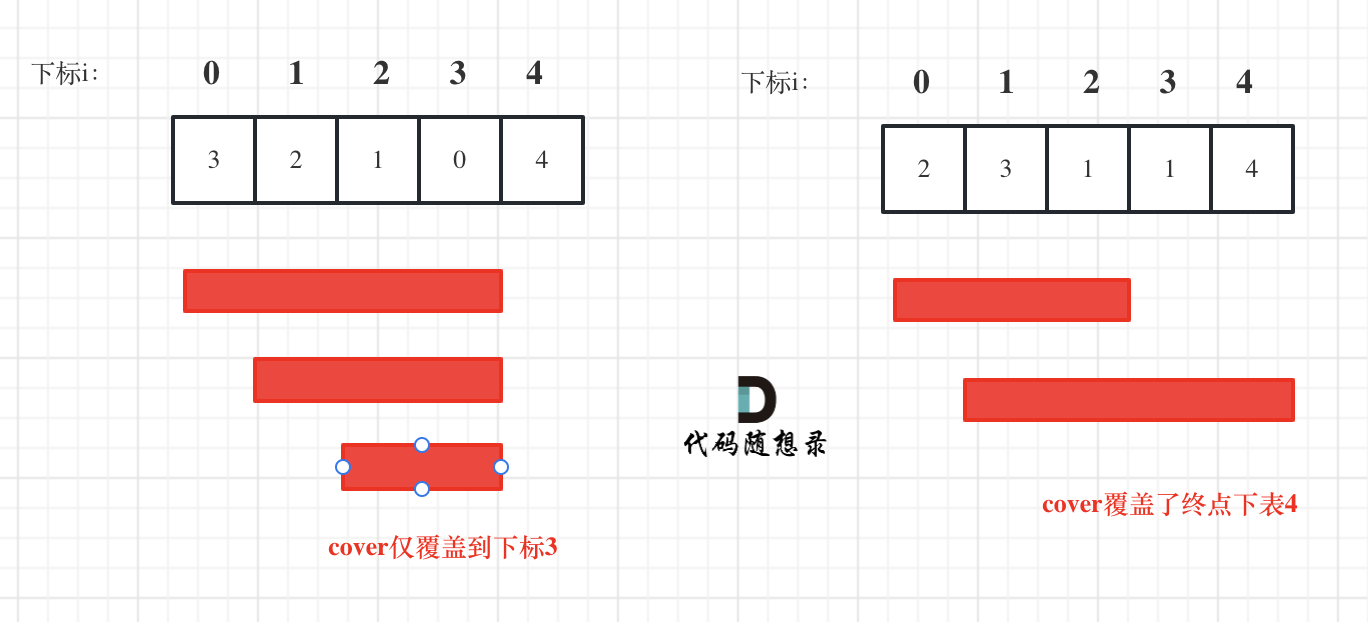
具体一些细节问题注意看代码。
答案:
class Solution { public boolean canJump(int[] nums) { if(nums.length == 1){ return true; } // 记录的是索引 int coverRange = 0; // 注意循环范围不是 nums.length!不然不管怎么样结果都是 true!况且可跳跃的范围本身就不能超过覆盖范围。 for(int i = 0; i <= coverRange; i++){ coverRange = Math.max(coverRange, i + nums[i]); if(coverRange >= nums.length - 1){ return true; } } return false; }}12.7:贪心算法-跳跃游戏II
题目:
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
- 输入: [2,3,1,1,4]
- 输出: 2
- 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明: 假设你总是可以到达数组的最后一个位置。
分析:
本题相较于上一题难了不少,但思路是相似的:别管怎么跳的,看覆盖范围即可。
其实通过模拟本题的示例就能发现,局部最优每次取尽可能大的步数不一定能得到整体最优解,因为实际上的局部最优不仅要考虑当前步的覆盖范围,还要考虑下一步的覆盖范围。
所以,局部最优:在当前这一步的覆盖范围下,使下一步的覆盖范围尽可能大。
整体最优:得到整体最大的、能到达终点的覆盖范围,得出最小步数。
在代码的书写中,如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
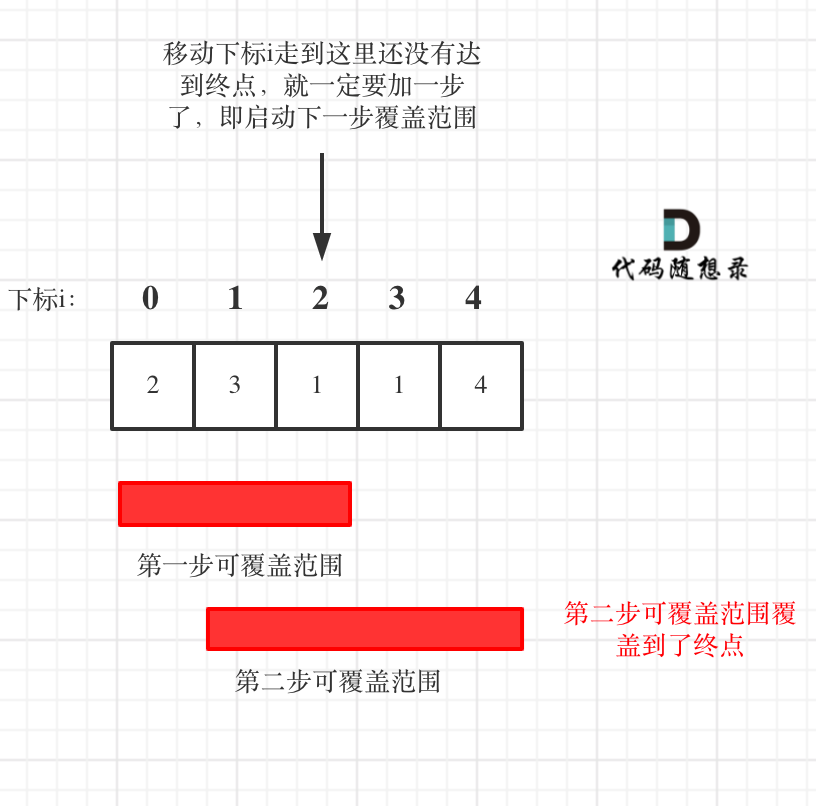
所以本题的关键在于:以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点。而不用管具体是怎么跳的。
答案:
class Solution { public int jump(int[] nums) { if(nums.length == 1){ return 0; } int curDistanceIndex = 0; int maxDistanceIndex = 0; int step = 0; for(int i = 0; i < nums.length; i++){ maxDistanceIndex = Math.max(nums[i] + i, maxDistanceIndex); if(i == curDistanceIndex){ step++; curDistanceIndex = maxDistanceIndex; if(curDistanceIndex >= nums.length - 1){ break; } } } return step; }}12.18:贪心算法-K次取反最大值
题目:
给定一个整数数组 A,我们只能用以下方法修改该数组:我们选择某个索引 i 并将 A[i] 替换为 -A[i],然后总共重复这个过程 K 次。(我们可以多次选择同一个索引 i。)
以这种方式修改数组后,返回数组可能的最大和。
示例 1:
- 输入:A = [4,2,3], K = 1
- 输出:5
- 解释:选择索引 (1) ,然后 A 变为 [4,-2,3]。
示例 2:
- 输入:A = [3,-1,0,2], K = 3
- 输出:6
- 解释:选择索引 (1, 2, 2) ,然后 A 变为 [3,1,0,2]。
示例 3:
- 输入:A = [2,-3,-1,5,-4], K = 2
- 输出:13
- 解释:选择索引 (1, 4) ,然后 A 变为 [2,3,-1,5,4]。
分析:
局部最优:让绝对值大的负数变为正数。如果K还剩奇数次,就让绝对值最小的正数变为负数。(K为偶数对正整数序列没有影响)(实际上局部贪心了两次)
全局最优:整个数组和达到最大。
答案:
class Solution { public int largestSumAfterKNegations(int[] nums, int k) { if(nums.length == 1) return nums[0]; Arrays.sort(nums); for(int i = 0; i < nums.length && k > 0; i++){ if(nums[i] < 0){ nums[i] = -nums[i]; k--; } } if(k % 2 == 1){ // 到这说明负数已经全部变为正数了,但k还剩奇数次。 // 将该正整数序列排序以后去找绝对值最小的正数反转。 Arrays.sort(nums); nums[0] = -nums[0]; } int sum = 0; for(int num : nums){ sum += num; } return sum; }}12.19:贪心算法-加油站
题目:
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
- 如果题目有解,该答案即为唯一答案。
- 输入数组均为非空数组,且长度相同。
- 输入数组中的元素均为非负数。
示例 1: 输入:
- gas = [1,2,3,4,5]
- cost = [3,4,5,1,2]
输出: 3 解释:
- 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
- 开往 4 号加油站,此时油箱有 4 – 1 + 5 = 8 升汽油
- 开往 0 号加油站,此时油箱有 8 – 2 + 1 = 7 升汽油
- 开往 1 号加油站,此时油箱有 7 – 3 + 2 = 6 升汽油
- 开往 2 号加油站,此时油箱有 6 – 4 + 3 = 5 升汽油
- 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
- 因此,3 可为起始索引。
示例 2: 输入:
- gas = [2,3,4]
- cost = [3,4,3]
- 输出: -1
- 解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油。开往 0 号加油站,此时油箱有 4 – 3 + 2 = 3 升汽油。开往 1 号加油站,此时油箱有 3 – 3 + 3 = 3 升汽油。你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。因此,无论怎样,你都不可能绕环路行驶一周。
分析:
这题有三种解法:
1. 暴力解法:
暴力的方法很明显就是O(n^2)的,遍历每一个加油站为起点的情况,模拟一圈。
如果跑了一圈,中途没有断油,而且最后油量大于等于0,说明这个起点是ok的。
暴力的方法思路比较简单,但代码写起来也不是很容易,关键是要模拟跑一圈的过程。
for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,要善于使用while!
C++代码如下:
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
for (int i = 0; i < cost.size(); i++) {
int rest = gas[i] - cost[i]; // 记录剩余油量
int index = (i + 1) % cost.size();
while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)
rest += gas[index] - cost[index];
index = (index + 1) % cost.size();
}
// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置
if (rest >= 0 && index == i) return i;
}
return -1;
}
};2. 不太贪心但是巧妙的全局贪心算法:
该算法考虑了三种情况:
- 情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
- 情况二:rest[i] = gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
- 情况三:如果累加的最小值是负数,汽车就要从最后的节点出发,从后向前,看哪个区间和能把这个负数填平,能把这个负数填平的节点就是出发节点。
针对情况三做个额外说明:因为是从头到尾累加,所以累加的最小负值一定是 0 到某个节点的区间和 [0 , k],从后向前遍历区间和,目的就是为了在到达 [0 , k] 这个区间之前,也就是 [k + 1 , gas.length – 1] 这个区间内找到一个可以把这个负数填平的区间和 [m , gas.length – 1],此时 m 就是出发节点。
3. 贪心算法
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量 rest[i] 为 gas[i] – cost[i]。
i 从 0 开始累加 rest[i],和记为 curSum,一旦 curSum 小于零,说明 [0, i] 区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从 i+1 算起,再从 0 计算 curSum。
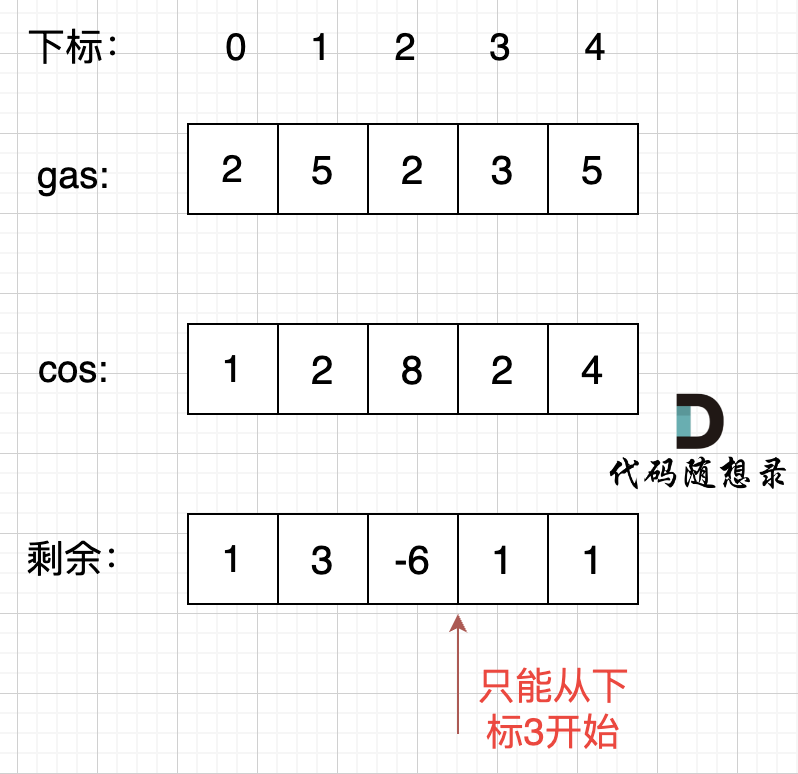
局部最优:当前累加 rest[i] 的和 curSum 一旦小于0,起始位置至少要是i+1。
全局最优:找到可以跑一圈的起始位置。
答案:
解法2.
class Solution { public int canCompleteCircuit(int[] gas, int[] cost) { int sum = 0; int min = 0; for (int i = 0; i < gas.length; i++) { sum += (gas[i] - cost[i]); min = Math.min(sum, min); } if (sum < 0) return -1; if (min >= 0) return 0; for (int i = gas.length - 1; i > 0; i--) { min += (gas[i] - cost[i]); if (min >= 0) return i; } return -1; }}解法3.
class Solution { public int canCompleteCircuit(int[] gas, int[] cost) { int curSum = 0; int totalSum = 0; int index = 0; for(int i = 0; i < gas.length; i++){ curSum += gas[i] - cost[i]; totalSum += gas[i] - cost[i]; if(curSum < 0){ index = i + 1; curSum = 0; } } if(totalSum < 0) return -1; return index; }}12.20:贪心算法-分发糖果
题目:
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
- 输入: [1,0,2]
- 输出: 5
- 解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
- 输入: [1,2,2]
- 输出: 4
- 解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
分析:
本题其实教会了我们一个道理:分析、解决问题的时候一定要条理清晰。
这道题你当然可以遍历所有节点,然后去考虑节点两边的大小关系。但是,更有条理、更简单、更高效的做法是先考虑一边(右大于左),再考虑另一边(左大于右)。
- 从前向后遍历,先确定右边评分大于左边的情况:
- 局部最优:只要右边评分比左边大,右边的孩子就多一个糖果。
- 全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果。
- 从后向前遍历,再确定左孩子大于右孩子的情况:
- 这里可能会有疑问,为什么不能从前向后遍历呢?就拿上图举例,显然 rating[5] 与 rating[4] 的比较要利用上 rating[5] 与 rating[6] 的比较结果,反之就会出问题,具体可以自己手推一下。
- 此时,还有一个细节必须要考虑:如果 ratings[i] > ratings[i + 1],此时 candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是 candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是 candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。粗略假设一下就能发现。
- 局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。
- 全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
答案:
class Solution { public int candy(int[] ratings) { int[] candyVec = new int[ratings.length]; candyVec[0] = 1; // 从前向后,右大于左 for(int i = 1; i < ratings.length; i++){ candyVec[i] = (ratings[i] > ratings[i - 1] ? candyVec[i - 1] + 1 : 1); } // 从后向前,左大于右 for(int i = ratings.length - 2; i >= 0; i--){ if(ratings[i] > ratings[i + 1]){ candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1); } } int sum = 0; for(int num : candyVec){ sum += num; } return sum; }}12.23:贪心算法-柠檬水找零(简单)
题目:
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。
顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
- 输入:[5,5,5,10,20]
- 输出:true
- 解释:
- 前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
- 第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
- 第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
- 由于所有客户都得到了正确的找零,所以我们输出 true。
示例 2:
- 输入:[5,5,10,10,20]
- 输出:false
- 解释:
- 前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。
- 对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。
- 对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。
- 由于不是每位顾客都得到了正确的找零,所以答案是 false。
提示:
- 0 <= bills.length <= 10000
- bills[i] 不是 5 就是 10 或是 20
分析:
这题其实很简单,只需要维护三种金额的数量,5,10和20即可。
有如下三种情况:
- 情况一:账单是5,直接收下。
- 情况二:账单是10,消耗一个5,增加一个10。
- 情况三:账单是20,优先消耗一个10和一个5,如果不够,再消耗三个5。
此时就会发现情况一和情况二都是固定策略,都不用我们来做分析了,而唯一不确定的其实在情况三。
情况三是带有贪心意识的,具体体现在账单是20的情况,为什么要优先消耗一个10和一个5呢?因为美元10只能给账单20找零,而美元5可以给账单10和账单20找零,美元5更万能!
局部最优:遇到账单20,优先消耗美元10,完成本次找零。
全局最优:完成全部账单的找零。
答案:
class Solution { public boolean lemonadeChange(int[] bills) { int five = 0; int ten = 0; for(int i = 0; i < bills.length; i++){ if(bills[i] == 5){ five++; }else if(bills[i] == 10){ five--; ten++; }else{ if(ten > 0){ ten--; five--; }else{ five -= 3; } } if(five < 0) return false; } return true; }}12.25:贪心算法-根据身高重建队列
题目:
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例:
- 输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
- 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
- 解释:
- 编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
- 编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
- 编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
- 编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
- 编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
- 编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
- 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
分析:
本题有两个维度,h和k。思考方式和分发糖果非常相似,当时我们就强调过遇到两个维度的时候,一定要先确定一个维度,再确定另一个维度。如果两个维度一起考虑一定会顾此失彼。
那先考虑哪一个维度呢?显然,先按照k排序并不合理,排完后调整起来非常麻烦。那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面,这样后续再按照k调整时就会变得很简单。具体效果如下图:

局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性。
全局最优:最后都做完插入操作,整个队列满足题目队列属性。
局部最优可推出全局最优,找不出反例,那就试试贪心。
答案:(代码写起来还是有点东西的)
class Solution { public int[][] reconstructQueue(int[][] people) { // 身高从大到小排(身高相同k小的站前面),这段排序 + lamba表达式使用的很巧妙。 Arrays.sort(people, (a, b) ->{ if(a[0] == b[0]) return a[1] - b[1]; // a - b 是升序排序。在a[0] == b[0]的下,根据k值升序排序。 return b[0] - a[0]; // b - a 是降序排序。a[0] != b[0]时,根据h值降序排序。 }); LinkedList<int[]> list = new LinkedList<>(); for(int[] p : people){ list.add(p[1],p); // Linkedlist.add(index, value),Linkedlist的插入用法。 } return list.toArray(new int[people.length][]); }}1.15:贪心算法-用最少数量的箭引爆气球(重叠区间问题)
题目:
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
- 输入:points = [[10,16],[2,8],[1,6],[7,12]]
- 输出:2
- 解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
- 输入:points = [[1,2],[3,4],[5,6],[7,8]]
- 输出:4
示例 3:
- 输入:points = [[1,2],[2,3],[3,4],[4,5]]
- 输出:2
示例 4:
- 输入:points = [[1,2]]
- 输出:1
示例 5:
- 输入:points = [[2,3],[2,3]]
- 输出:1
分析:
细想一下就会发现,使弓箭使用最少的方法就是让气球尽可能重叠。尽可能重叠,那就试试贪心吧。
局部最优:当气球出现重叠,一起射,所用弓箭最少。
全局最优:把所有气球射爆所用弓箭最少。
算法确定下来了,那么如何模拟气球射爆的过程呢?是在数组中移除元素还是做标记呢?
如果真实的模拟射气球的过程,应该射一个,气球数组就remove一个元素,这样最直观,毕竟气球被射了。
但仔细思考一下就发现:如果把气球排序之后,从前到后遍历气球,被射过的气球仅仅跳过就行了,没有必要让气球数组remove气球,只要记录一下箭的数量就可以了。
为了让气球尽可能的重叠,需要对数组进行排序。
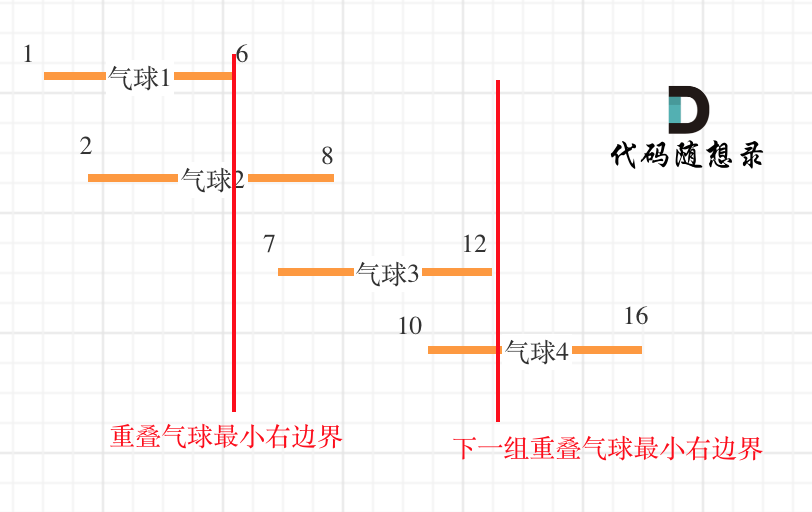
接下来只要不断去判断上一个气球集的最小右边界是否与下一个气球左边界重叠就行了(这里就体现了贪心,每一次完整的遍历都是从头开始寻找重叠的最大部分的气球,由每一部分的局部最优得到全局最优)。
这类题型的思路在下一题更能得到体现。
答案:
class Solution { public int findMinArrowShots(int[][] points) { Arrays.sort(points, (a, b) -> Integer.compare(a[0],b[0])); int count = 1; for(int i = 1; i < points.length; i++){ if(points[i - 1][1] > points[i][0]){ points[i][1] = Math.min(points[i - 1][1], points[i][1]); }else{ count++; } } return count; }}
1.16:贪心算法-无重叠区间
题目:
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
- 输入: [ [1,2], [2,3], [3,4], [1,3] ]
- 输出: 1
- 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
- 输入: [ [1,2], [1,2], [1,2] ]
- 输出: 2
- 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
- 输入: [ [1,2], [2,3] ]
- 输出: 0
- 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
分析:
这道题和上一道射气球题的思路很像,都是要计算有多少重叠区间。
显然,按照左边界做升序排序会方便很多。(下图是右边界升序排序,思路是一样的,但是很不方便,要考虑更多细节)

当确定区间 1 和 区间2 重叠后,如何确定是否与 区间3 也重贴?只要取 区间1 和 区间2 右边界的最小值,因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分,如果这个最小值也触达到区间3,那么说明 区间 1,2,3都是重合的。
以此类推,直到上一个区间集右边界的最小值不再大于下一个区间的左边界。
这个时候我们默认上一个区间集的重叠区间已经被删除(实际上我们只计数就行了,不需要真的从区间集中移除重叠区间)。
这里就体现出了贪心的思想:
局部最优:找到每个重叠区间集,并删除对应的重叠区间。
全局最优:找到需要移除区间的最小数量。
答案:
public int eraseOverlapIntervals(int[][] intervals) { Arrays.sort(intervals, (a,b)-> { return Integer.compare(a[0],b[0]); // 升序 }); int remove = 0; int preTailMin = intervals[0][1]; for(int i = 1; i < intervals.length; i++){ if(preTailMin > intervals[i][0]){ remove++; preTailMin = Math.min(intervals[i][1], preTailMin); }else{ preTailMin = intervals[i][1]; } } return remove;}1.17:贪心算法-划分字母区间(比较巧妙)
题目:
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
- 输入:S = “ababcbacadefegdehijhklij”
- 输出:[9,7,8] 解释: 划分结果为 “ababcbaca”, “defegde”, “hijhklij”。 每个字母最多出现在一个片段中。 像 “ababcbacadefegde”, “hijhklij” 的划分是错误的,因为划分的片段数较少。
分析:
这道题其实和贪心关系不大,有两种解法,一种是非常巧妙的、不太容易想到的用最远距离圈字符的解法,还有一种是延续前两道重叠区间的思想。
第一种:
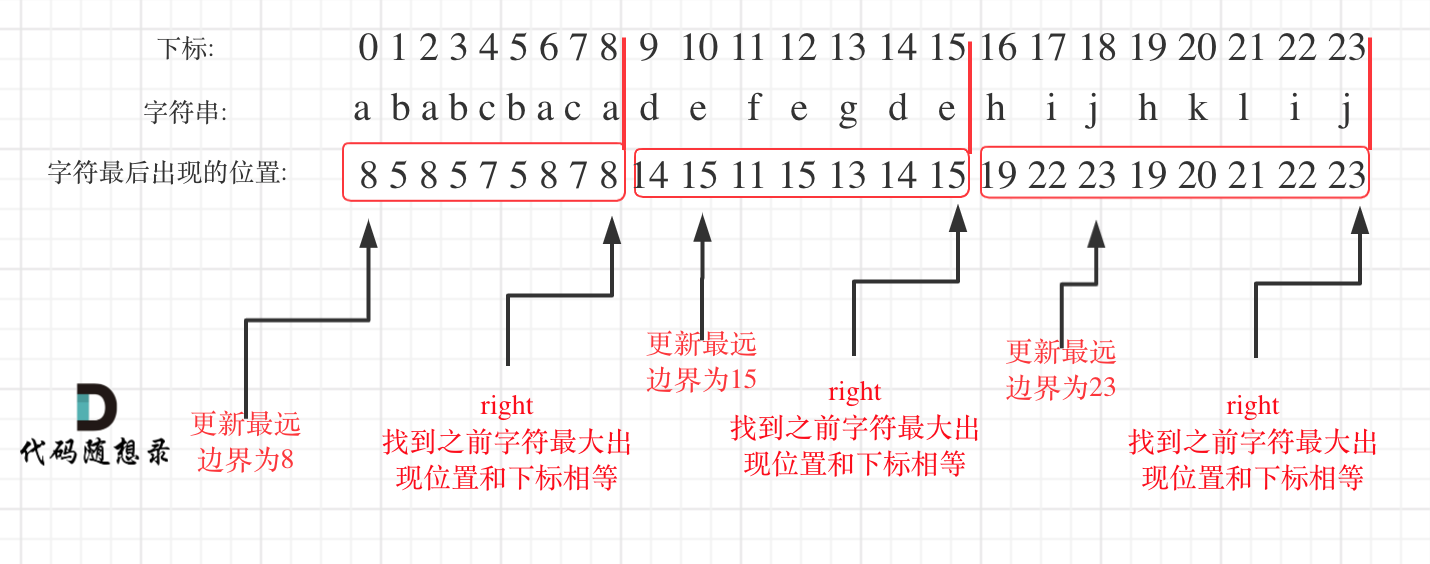
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
答案:
public List<Integer> partitionLabels(String S) {
List<Integer> list = new LinkedList<>();
int[] edge = new int[26];
char[] chars = S.toCharArray();
for (int i = 0; i < chars.length; i++) {
edge[chars[i] - 'a'] = i;
}
int idx = 0;
int last = -1;
for (int i = 0; i < chars.length; i++) {
idx = Math.max(idx,edge[chars[i] - 'a']);
if (i == idx) {
list.add(i - last);
last = i;
}
}
return list;
}
第二种:
统计字符串中所有字符的起始和结束位置,记录这些区间。将区间按左边界从小到大排序,如果找到一个边界能在分割的过程中不切割其包含的其他区间,那这个边界就是答案。
答案:
class Solution{
public int[][] findPartitions(String s) {
List<Integer> temp = new ArrayList<>();
int[][] hash = new int[26][2];//26个字母2列 表示该字母对应的区间
for (int i = 0; i < s.length(); i++) {
//更新字符c对应的位置i
char c = s.charAt(i);
if (hash[c - 'a'][0] == 0) hash[c - 'a'][0] = i;
hash[c - 'a'][1] = i;
//第一个元素区别对待一下
hash[s.charAt(0) - 'a'][0] = 0;
}
List<List<Integer>> h = new LinkedList<>();
//组装区间
for (int i = 0; i < 26; i++) {
//if (hash[i][0] != hash[i][1]) {
temp.clear();
temp.add(hash[i][0]);
temp.add(hash[i][1]);
//System.out.println(temp);
h.add(new ArrayList<>(temp));
// }
}
// System.out.println(h);
// System.out.println(h.size());
int[][] res = new int[h.size()][2];
for (int i = 0; i < h.size(); i++) {
List<Integer> list = h.get(i);
res[i][0] = list.get(0);
res[i][1] = list.get(1);
}
return res;
}
public List<Integer> partitionLabels(String s) {
int[][] partitions = findPartitions(s);
List<Integer> res = new ArrayList<>();
Arrays.sort(partitions, (o1, o2) -> Integer.compare(o1[0], o2[0]));
int right = partitions[0][1];
int left = 0;
for (int i = 0; i < partitions.length; i++) {
if (partitions[i][0] > right) {
//左边界大于右边界即可进行一次分割
res.add(right - left + 1);
left = partitions[i][0];
}
right = Math.max(right, partitions[i][1]);
}
//最右端
res.add(right - left + 1);
return res;
}
}
1.18:贪心算法-合并区间
题目:
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
- 输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
- 输出: [[1,6],[8,10],[15,18]]
- 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
- 输入: intervals = [[1,4],[4,5]]
- 输出: [[1,5]]
- 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
分析:
这题很容易看出其实还是判断重叠区间的问题。判断重叠的逻辑和前面的射气球、无重叠区间基本一样,都是先排序,再用当前区间集的最大右边界去和下一个区间的左边界去做比较,只是这次判断相等的时候也算是区间重叠。
还有一个区别就是判断区间重叠后的逻辑,也就是如何模拟合并区间。只要用合并区间后的左边界和右边界作为一个新的区间,加入到result数组里就可以了。
答案:
class Solution { public int[][] merge(int[][] intervals) { List<int[]> res = new LinkedList<>(); Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0])); int start = intervals[0][0]; int end = intervals[0][1]; for (int i = 1; i < intervals.length; i++) { //如果左边界大于最大右边界 if (intervals[i][0] > end) { //加入区间 并且更新start res.add(new int[]{start, end}); start = intervals[i][0]; end = intervals[i][1]; } else { //更新最大右边界 end = Math.max(end, intervals[i][1]); } } res.add(new int[]{start, end}); return res.toArray(new int[res.size()][]); }}1.19:贪心算法-单调递增的数字
题目:
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
(当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。)
示例 1:
- 输入: N = 10
- 输出: 9
示例 2:
- 输入: N = 1234
- 输出: 1234
示例 3:
- 输入: N = 332
- 输出: 299
分析:
题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。
例如:98,一旦出现strNum[i – 1] > strNum[i]的情况(非单调递增),首先想让strNum[i – 1]–,然后strNum[i]给为9(这里就有一些贪心的思想了,每一次判断都在保证单调递增的情况下让数字尽可能大),这样这个整数89就是小于98的最大的单调递增整数。
这题还要考虑一点,就是从前向后遍历还是从后向前遍历。
如果从前向后遍历,遇到strNum[i – 1] > strNum[i]的情况,让strNum[i – 1]减一,但此时如果strNum[i – 1]减一了,可能又小于strNum[i – 2]。举个例子,数字332从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,而真正的结果应该是299。
所以真正的遍历顺序应该是从后向前遍历,因为可以重复利用上次比较得出的结果,这样上个例子332的数值变化就变为:332 -> 329 -> 299。
答案:
class Solution { public int monotoneIncreasingDigits(int n) { String s = String.valueOf(n); char[] chars = s.toCharArray(); int start = s.length(); for (int i = s.length() - 2; i >= 0; i--) { if (chars[i] > chars[i + 1]) { chars[i]--; start = i+1; } } for (int i = start; i < s.length(); i++) { chars[i] = '9'; } return Integer.parseInt(String.valueOf(chars)); }}1.20:贪心算法-监控二叉树(较复杂)
题目:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

- 输入:[0,0,null,0,0]
- 输出:1
- 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
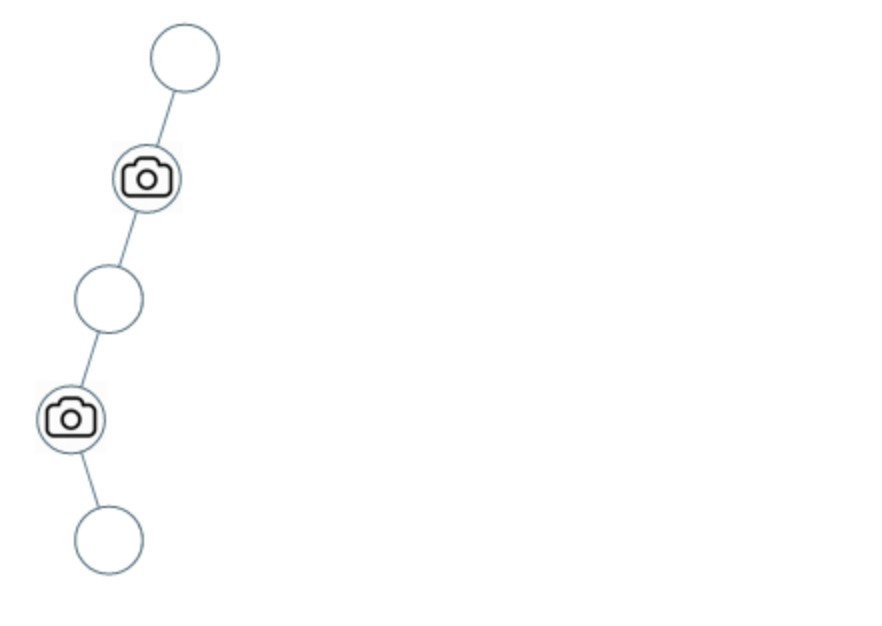
- 输入:[0,0,null,0,null,0,null,null,0]
- 输出:2
- 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
分析:
这道题其实思路也还好(当然想到正确的思路还是比较难的),但是它复杂就复杂在这是一棵二叉树,需要对二叉树的操作非常娴熟,并且还涉及到状态转移?其实就是要分类讨论,根据不同的情况做不同的操作,而且这种情况还很多,所以做起来很不容易,思路必须非常清晰。因为思路整理起来比较复杂,所以建议直接看别人完整的解析。
答案:
class Solution {
static int ans;
public int minCameraCover(TreeNode root) {
ans = 0; // 初始化
if(f(root) == 0) ans ++;
return ans;
}
// 定义 f 函数有三种返回值情况
// 0:表示 x 节点没有被相机监控,只能依靠父节点放相机
// 1:表示 x 节点被相机监控,但相机不是放在自身节点上
// 2:表示 x 节点被相机监控,但相机放在自身节点上
public static int f(TreeNode x) {
if(x == null) return 1; // 空树认为被监控,但没有相机
// 左右递归到最深处
int l = f(x.left);
int r = f(x.right);
// 有任意一个子节点为空,就需要当前节点放相机,不然以后没机会
if(l == 0 || r == 0) {
ans ++; // 放相机
return 2;
}
// 贪心策略,左右子树都被监控,且没有监控到当前节点,
// 那么最有利的情况就是将相机放置在当前节点父节点上,
// 因为这样能多监控可能的子树节点和父父节点
if(l == 1 && r == 1) return 0;
// 剩下情况就是左右子树有可能为 2,即当前节点被监控
return 1;
}
}